Linear Equations and Inequalities

Content

• Introduction
• Slope
• Writing Linear Equations
  • Slope-Intercept Form
  • Standard Form
  • Point-Slope Form
• Graphing Linear Equations
• Parallel and Perpendicular Lines
• Direct Variation
• Graphing Linear Inequalities

Introduction

A linear equation is the equation of a line, and the graphs of linear equations always display a straight line. All linear equations must include variables such as x and y and may include a constant or coefficient to a variable but there will be no exponent.

Here is an example of a linear equation and some points on the line $y=2x +4$. A chart is a handy tool you can use to create a list of some of the ordered pairs of an equation. Because the equation is linear, the graph of this set of points is a straight line.

$y=2x +4$

$\begin{array}{|lrl|} \hline&&\\[-3mm] & \mathbf{x}& \mathbf{y}\\[0.5mm] \hline&&\\[-3mm] & -2 & 0\\[0.5mm] & -1 & 2\\[0.5mm] & 0 & 4\\[0.5mm] & 1 & 6\\[0.5mm] & 2 & 8\\[0.5mm] \hline \end{array}$

Slope

The slope of a line is the slant or incline of a line. Slope can be a positive or negative number.The symbol m is used to represent the slope. Use the slope formula to calculate the value of the slope equal to the change of y divided by the change of x.

$m=\frac{y_2-y_1}{x_2-x_1}$

Example: Find the slope of the line that passes through points (2, 11) and (3, 9).

$m=\frac{9-11}{3-2} = \frac{-2}{1}= -2$

The slope is equal to -2. The negative sign indicates a downward slope.

Writing Linear Equations

Although there are several formulas for writing equations of lines, linear equations are most often presented in the Slope-Intercept form.

Slope-Intercept Form

$y=mx+b$

• m is the slope of the line
• b is the y-intercept

Standard Form

The standard form of a line is another format to present the same information as the slope-intercept form.

$Ax+By=C$
A, B, and C are coefficients or constants.

To change from standard form to slope-intercept form, use opposite operations to move the terms.

$\begin{align} Ax+By&=C\\ -3x + y &= 16\\ -3x +3x + y &= 16 +3x\\ y &= 3x +16 \end{align}$

$\begin{align} y&=mx+b\\ y &= 3x +16 \end{align}$

Writing the equation in the slope-intercept form makes it easier to determine the slope of this line is 3, and the y-intercept is 16.

Point-Slope Form

The point-slope form is used to calculate an unknown point when the slope and one point on the line is known.

$ (y-y_1)=m(x-x_1)$

y and x are unknown values. $y_1$ and $x_1$ are a known ordered pair.

Use the point-slope form to write the equation of the line with a slope of 1 and passing through point (3, 4).

$\begin{align} (y-y_{1})&=m(x-x_{1})\\ (y-4)&=1(x-3)\\ y -4 &= x -3\\ y - 4 + 4 &= x -3 +4\\ y&=x + 1 \end{align}$

Graphing Linear Equations

Use the information found in the equation of a line written in slope-intercept form to create the matching graph.

$\begin{align} y&=mx+b\\ y &= 2x +3 \end{align}$

For this linear equation, the slope is 2 and the y-intercept is 3.

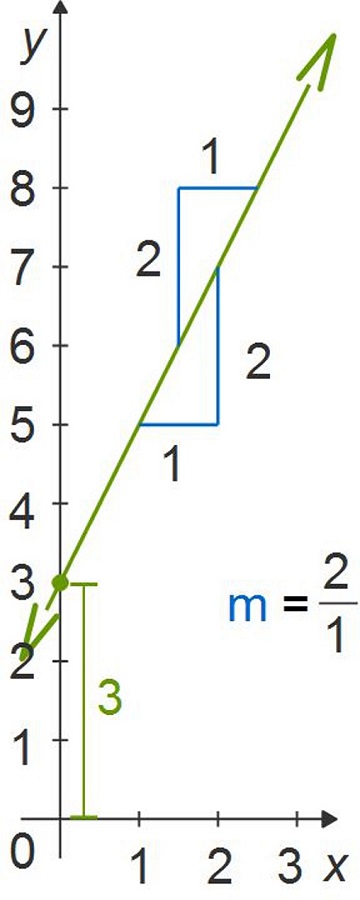
Parallel and Perpendicular Lines

The slope can be used to indicate if lines are parallel or perpendicular:

• Parallel lines: slopes are equal
• Perpendicular lines: slopes are negative inverses

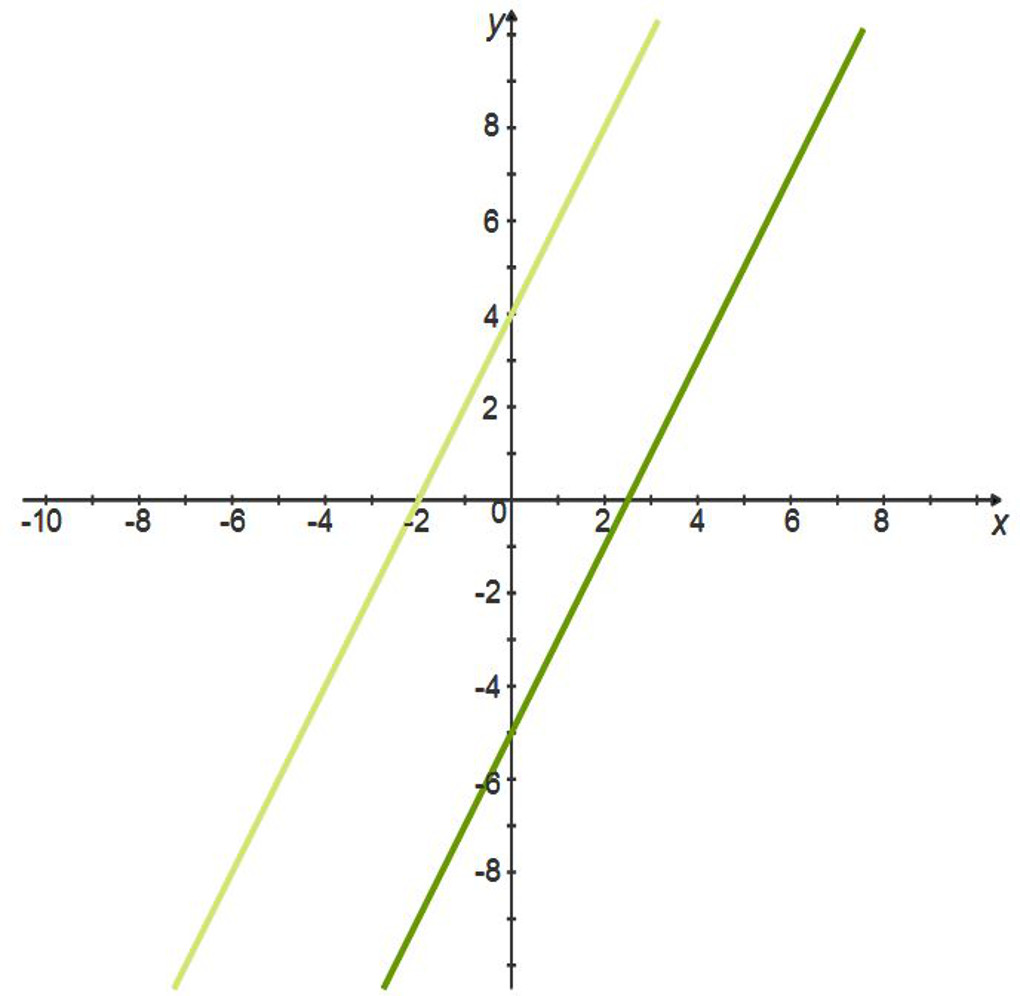
Example: For this problem, are the slopes parallel or perpendicular? Compare the equation of two lines. What do you know about the slopes?

$\begin{align} y&=2x +4\\ y&=2x -5 \end{align}$

The slopes are the same, so the lines are parallel.

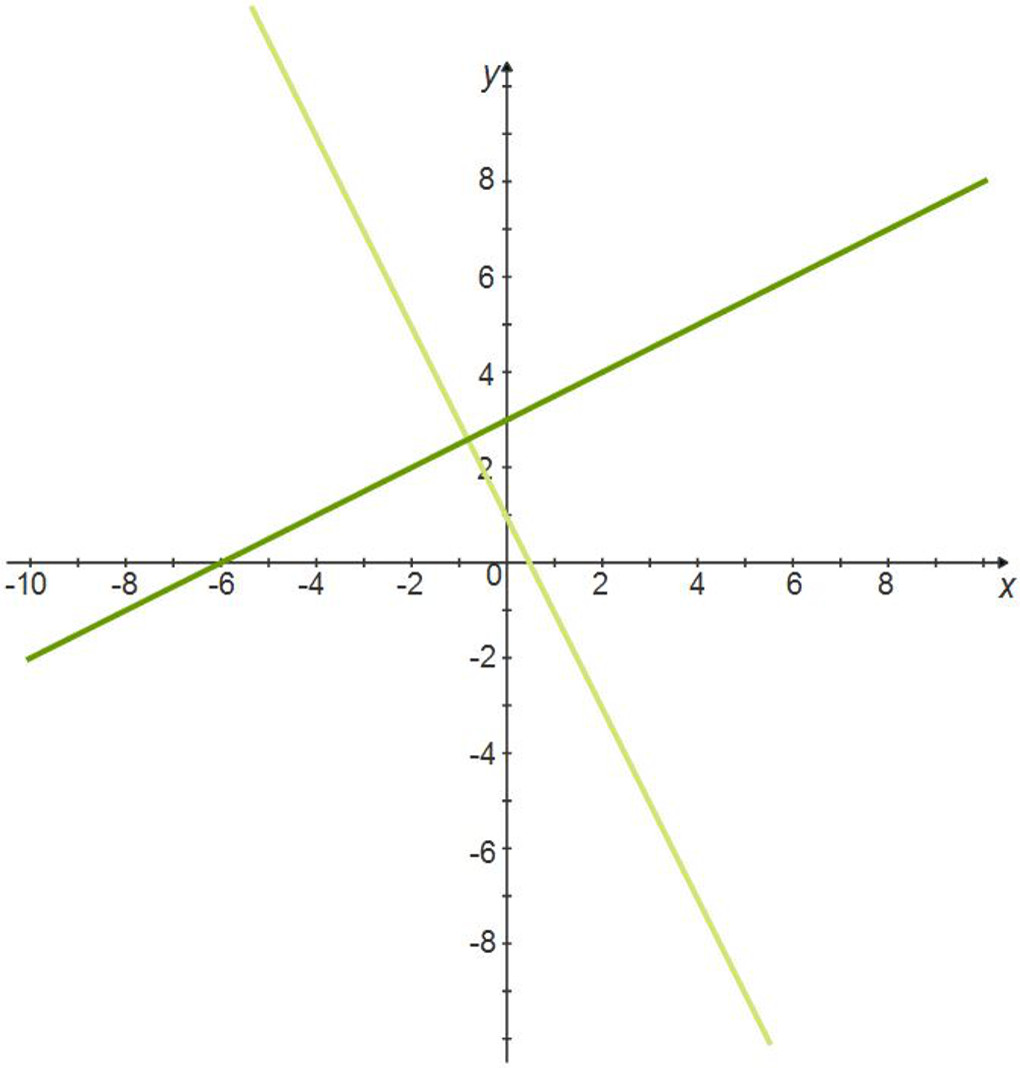
$\begin{align} y&= -2x+1\\ y&=\frac{1}{2}x+3\\ \end{align}$

The slopes are negative inverses (the product of the two slopes is equal to -1), so the lines are perpendicular.

Direct Variation

When the value of y varies with the value of x, there is a direct variation. The formula for direct variation is:

$\begin{align} y&= k\times x\\ y&= kx \end{align}$

k is the constant of variation. The formula for k is: $k=\frac{y}{x}$

Example: This problems demonstrates a real world use of direct variation. A car gets 20 miles per gallon. How many gallons of gas are needed to travel a distance of 2,400 miles? Use the direct variation to solve for x.

$\begin{align} y&= kx\\ y&=20x\\ 2,\!400 &= 20x\\ \frac{2,\!400}{20} &= \frac{20}{20}x\\ x&=120 \end{align}$

With a constant of variation of 20, the car will need 120 gallons to travel 2,400 miles.

Graphing Linear Inequalities

Graphing linear inequalities is a multi-step process. First graph the line. Then determine if the graph includes the line and if the solution set is above or below the line.

Example 1: For this inequality, the line is not included, and the solution set is below the line. $y<3x +4$

Example 2: But for this inequality, the line is included, and the solution set is above the line. $y\geq\frac{1}{2}x +5$.